This time, let's look at the 'Mass moment of inertia'.
Unlike the 'Geometrical moment of inertia',
Mass is used instead of Geometrical for the 'Mass moment of Inertia'.
Mass is about the inertia of an object, that is,
the property of trying to sustain a movement around mass.
And when 'moment' is attached to it, it shows the property of
continuing the rotational motion of the center of mass.

When an external force 'F' is generated that rotates an object
with a mass of 'm' based on the rotational axis as shown in Fig. 1 below.

According to Newton's law, acceleration occurs
in the tangential direction as shown in Equation 1 below.

The moment for micro-mass due to external force is as shown in Equation 2 below.

The acceleration (a) is the product of the turning radius (r) and
the angular acceleration (α).
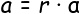
Substituting Equation.3 to Equation.1, Equation.4 is

Substituting into Equation.2 again, it is as shown in Equation.5 below.

Integrating Equation 5 to find the total moment.

Here, 'I' is called the mass 'Moment of inertia'.

As mentioned earlier,
The 'Mass moment of inertia' is inertia in the rotational motion of the center of mass.
In other words, it is a property that resists rotational motion.
The object in Fig. 1 above can be changed to
an equivalent model in the form of Fig. 2 below.

That is, if an object with the same mass is placed
at an appropriate distance (d), an equivalent model
with the mass moment of inertia as shown in Fig. 1 can be obtained.
Assuming the two models have the same mass moment of inertia,

The summary of 'd' is as in Eq. 9.

In this case, 'd' is referred to as the rotaional radius.
When rotating an object based on an arbitrary position,
if only the mass is considered, the radius of rotation
can be obtained to have the same 'Mass moment of inertia'.
In addition, the 'parallel axis theorem' applies equally
to the 'Mass moment of inertia' as for the 'Geometrical moment of inertia'.


Also, the relationship between the 'Polar moment of inertia' and
the 'Right angle moment of inertia' is also the same
as that mentioned in the 'Geometrical moment of inertia'.

Thank you. ^^