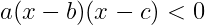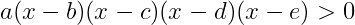수학2 - 2. 고차부등식과 분수부등식
- 수학/수학2
- 2022. 4. 25.
반응형
2-1. 고차부등식 - 이차부등식 |
: 이차 다항식을 포함한 부등식을 의미하며
: 일차항으로 인수분해가 가능한 경우
- 모든 항을 좌변으로 이항한 후
- 좌변을 인수분해하여 아래의 꼴로 만든다.

: 단, 등호(=)가 있을 경우 x축과 만나는 점도 해에 포함됨
: 그래프에서 범위가 헷갈릴 경우 계산이 쉬운 임의의 점을 방정식에 대입하여 확인
| 구분 | |||
| a > 0 | b > c |  |
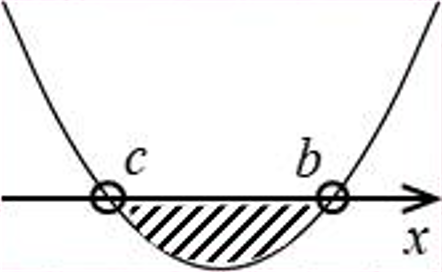 |
| 해는 x < c , x > b | 해는 c < x < b | ||
| b = c |  |
 |
|
| x의 해는 실수 전체 (단, x ≠ b) | 해가 없음 | ||
| a < 0 | - | 위의 그래프가 x축을 기준으로 위, 아래가 반전되며 풀이는 동일함 | |
2-2. 고차부등식 - 삼차부등식 |
: 삼차 다항식을 포함한 부등식을 의미하며
: 일차항으로 인수분해가 가능한 경우
- 모든 항을 좌변으로 이항한 후
- 좌변을 인수분해하여 아래의 꼴로 만든다.

: 단, 등호(=)가 있을 경우 x축과 만나는 점도 해에 포함됨
: 그래프에서 범위가 헷갈릴 경우 계산이 쉬운 임의의 점을 방정식에 대입하여 확인
| 구분 | |||
| a > 0 | b > c > d |  |
 |
| d < x < c , x > b | x > d , c < x < b | ||
| b > c = d |  |
 |
|
| x > b | x < b (단, x ≠ c) | ||
| b = c > d |  |
 |
|
| x > d (단, x ≠ b) | x < d | ||
| b = c = d |  |
 |
|
| x > b | x < b | ||
| a < 0 | - | 위의 그래프가 x축을 기준으로 위, 아래가 반전되며 풀이는 동일함 | |
2-3. 고차부등식 - 사차부등식, 오차부등식 개형 |
| 구분 | 풀이 방법 |
| 사차부등식 (a > 0) |
|
 |
|
| 오차부등식 (a > 0) |
|
 |
2-4. 고차부등식 - 인수분해 불가능 시 |
: 일차항으로 인수분해가 불가능한 경우
- 모든 항을 좌변으로 이항한 후
- 좌변을 가능한만큼 인수분해하고
- 아래 식.3의 동치 관계를 적용한다.
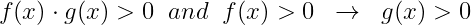
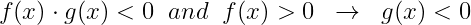
예)
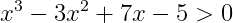
식.4를 인수분해하면 아래 식.5가 된다.
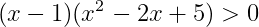
식.5의 이차항은 식.6과 같이 0보다 크므로
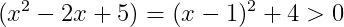
결과적으로
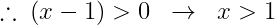
2-5. 분수부등식 |
: 미지수 x에 관한 분수식을 포함한 부등식을 의미하며
: 다음의 순서대로 풀이한다.
- 모든 항을 좌변으로 이항한 후
- 좌변을 f(x)/g(x) 꼴로 변형하고
- 아래의 동치 관계를 적용한다.
| 구분 | 동치 관계 |
 |
|
 |
|
 |
|
 |