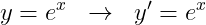수학2 - 6. 변화율과 도함수

6-1. 변화율과 도함수의 정의

1. 변화율

구분	정의
평균변화율	= 직선 PQ의 기울기 = y증분 / x증분
(순간)변화율 = 미분계수	= 정해진 점 P에서 접선의 기울기 = 극한값
	이 극한값을 아래와 같이 표현함
	'미분계수'란? (微 : 작을 미, 分 : 나눌 분) : △x→0일 때, 즉 x증분을 미세하게 나눈 모든 점에서의 기울기 : dx, dy에서 d는 미분과 같은 의미를 가짐 (divide)

 

2. 도함수

도함수	변화율을 x의 함수로 나타낸 것으로써, 아래의 극한값이 존재할 때
	다음 식과 같이 표현함
	즉, 임의의 점 P에서 접선의 기울기

---

6-2. 미분법 공식

1. 기본 공식

구분	공식
기본 (c : 상수 ,  n : 실수)
합성 함수	y=f(u), u=g(x) 가 미분 가능할 때, y=f(g(x))도 미분 가능함

 

2. 음함수, 매개변수

구분	공식
음함수	F(x, y)=0의 형태를 갖는 함수를 미분할 때, 아래의 공식을 적용함
	아래의 예를 참조하세요.
매개변수로 표현된 함수	변수 x, y가 각각 매개변수 t로 표현된 함수 x=f(t), y=g(t)가 미분 가능할 때, 매개변수 t를 소거하지 않고도 미분이 가능함

 

3. 삼각함수, 지수함수, 로그함수

구분	공식
삼각함수
지수함수
로그함수

---

6-3. 고계도함수 (n계도함수)

고계도함수 미분

식.1

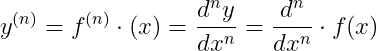
예)

식.2 5차 함수

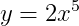
구분	도함수
1계
2계
3계
4계
5계

수학2_6. 변화율과 도함수_연습 문제1.JPG

0.06MB

수학2_6. 변화율과 도함수_연습 문제2.JPG

0.05MB