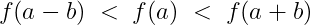수학2 - 9. 미분과 극대, 극소
- 수학/수학2
- 2022. 5. 3.
반응형
9-1. 함수의 증가, 감소 상태 |
1. 함수의 증가 상태
| 구분 | 내용 | 그래프 |
| 증가 상태-1 | 함수 f(x)에서 양수 b에 대하여 아래 식을 만족하면 'x=a'에서 증가 상태이다. |
 |
| 증가 상태-2 | 일정 구간에서 함수 f(x)가 미분 가능하고, 아래 식을 만족하면 그 구간에서 증가 상태이다. |
|
| 역) 함수 f(x)가 미분 가능하고 그 구간에서 증가 상태라면 아래 식을 만족한다. | ||
2. 함수의 감소 상태
| 구분 | 내용 | 그래프 |
| 감소 상태-1 | 함수 f(x)에서 양수 b에 대하여 아래 식을 만족하면 'x=a'에서 감소 상태이다. |
 |
| 감소 상태-2 | 일정 구간에서 함수 f(x)가 미분 가능하고, 아래 식을 만족하면 그 구간에서 감소 상태이다. |
|
| 역) 함수 f(x)가 미분 가능하고 그 구간에서 감소 상태라면 아래 식을 만족한다. | ||
3. 함수의 일정한 상태
: 일정한 구간에서 함수 f(x)가 미분 가능하고, f'(x)=0 을 만족한다면 그 구간에서 일정한 값을 가진다.
: 즉, 상수이다.
9-2. 함수의 극대, 극소 |

1. 함수의 극대
| 구분 | 내용 |
| 극대-1 | 연속함수인 f(x)가 'x=a'에서 상태가 변할 때, 증가 → 감소 상태로 변한다면 'x=a'에서 '극대' 라 하며 f(a)는 '극댓값' 이라 한다. |
| 극대-2 | f'(a)=0이고 'x=a'를 기점으로 f'(x)의 값이 (+) → (-)로 변한다면 'x=a'에서 '극대' 라 하며 f(a)는 '극댓값' 이라 한다. |
2. 함수의 극소
| 구분 | 내용 |
| 극소-1 | 연속함수인 f(x)가 'x=a'에서 상태가 변할 때, 감소 → 증가 상태로 변한다면 'x=a'에서 '극소' 라 하며 f(a)는 '극솟값' 이라 한다. |
| 극소-2 | f'(a)=0이고 'x=a'를 기점으로 f'(x)의 값이 (-) → (+)로 변한다면 'x=a'에서 '극소' 라 하며 f(a)는 '극솟값' 이라 한다. |
3. 2계 미분을 통한 극대, 극소 판별
| 구분 | 내용 |
| 극대 | f'(a)=0 이고 f''(a)<0이면, 'x=a' 에서 '극대' 이다. |
| 극소 | f'(a)=0 이고 f''(a)>0이면, 'x=a' 에서 '극소' 이다. |
9-3. 곡선의 요철, 변곡점 |
1. 곡선의 요철
함수 y=f(x)가 일정 구간에서
| 조건 | 요철 형태 |
| f''(x) > 0 | 아래로 볼록 |
| f''(x) < 0 | 위로 볼록 |
(*요철 凹: 오목할 요, 凸: 볼록할 철 / 오목함과 볼록함)
2. 변곡점
f''(a) = 0 이고 'x=a' 를 기점으로 f''(x)의 부호가 바뀌는 경우, 점 (a, f(x))를 함수 f(x)의 '변곡점' 이라 한다.
9-4. 곡선의 개형 |
: 곡선의 개형을 확인하여 주어진 함수를 한 눈에 알아볼 수 있습니다.
: 아래의 순서로 곡선의 개형을 그립니다.
① 곡선의 범위를 확인
② 곡선과 x, y축의 교점을 확인
③ 함수를 1계 미분하여 f'(x)를 통해 '극대, 극소, 증가, 감소' 확인
④ 함수를 2계 미분하여 f''(x)를 통해 곡선의 요철 방향과 변곡점 확인
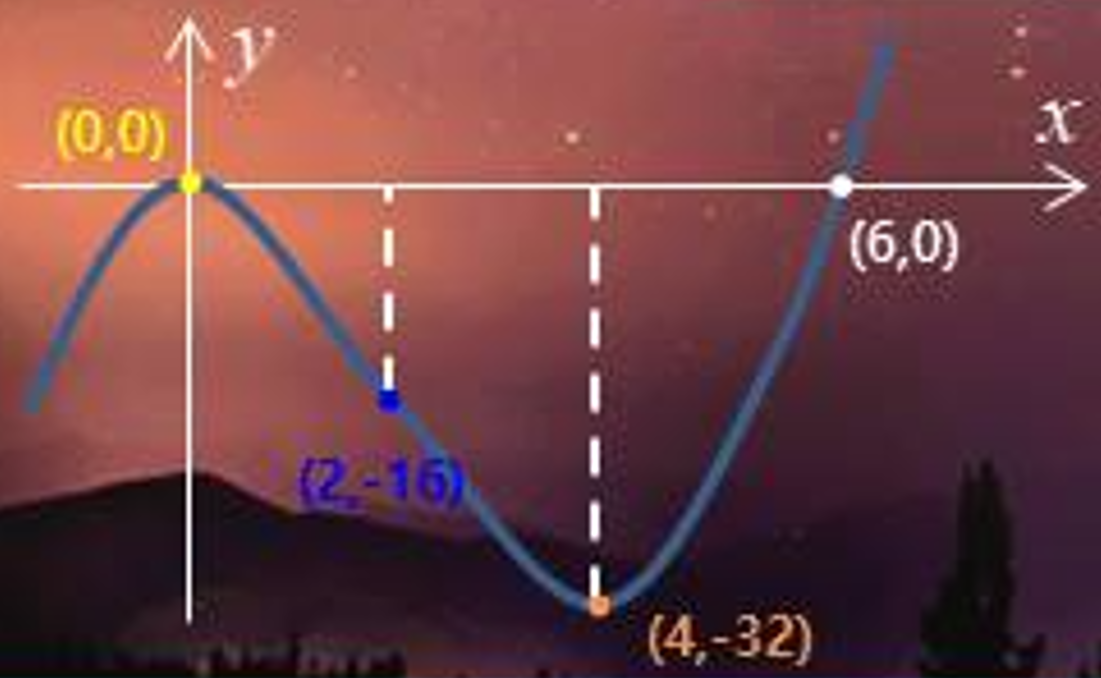
예) 식.1에 있는 함수의 개형은?
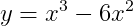
1계, 2계 미분 방정식은 아래 식.2와 같습니다.
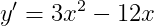
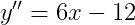
곡선 그래프의 개형을 표로 나타내보면
| x | -∞ | ~ | 0 | ~ | 2 | ~ | 4 | ~ | 6 | +∞ |
| y' | (+) | 0 | (-) | (-) | (-) | 0 | (+) | (+) | ||
| y'' | (-) | (-) | (-) | 0 | (+) | (+) | (+) | (+) | ||
| y | -∞ | 0 (극대) |
-16 (변곡점) |
-32 (극소) |
0 | +∞ |
위 표를 바탕으로 그래프의 개형을 그리면 아래와 같습니다.